We are given two points of a line
(-2, -2) and (1,4)
Equation of line:
Firstly , we will find slope
(-2, -2) and (1,4)
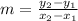
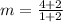
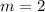
now, we can find equation of line
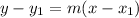
now, we can plug values
and we get
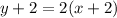
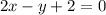
Distance:
now, we can use distance formula
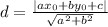
firstly , we will find a and b
a=2 and b=-1
point is (6,-1)
so, xo=6 and yo=-1
we can plug values
and we get
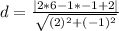
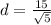
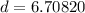 ...........Answer
...........Answer