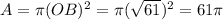Question

In figure 2, O is the center of the circle and B is a point on the circle. In rectangle OABC, if OA-5 and OC -6, what is the area of the circle?

A) 11 pie
B) 25 pie
C) 36 pie
D) 61 pie

Answer 1

We will use the following two facts:

1) Since ABCO is a rectangle, the two diagonals AC and OB are the same length

2) Since O is the center of the circle and B is a point on the circumference, OB is a radius of the circle.

We can compute the length of AC, since we know the length of OA and OC: in fact, OAC is a right triangle of which we know the two legs. So, we have

`AC = √(OA^2+OC^2) = √(5^2+6^2) = √(25+36) = √(61)`

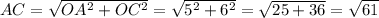
Invoking the point (1), we can deduce that
`OB=AC = √(61)`

The area of a circle is given by the following formula:

`A = \pi r^2`

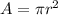
And by point (2), we know that OB is a radius, so we have

`A = \pi (OB)^2 = \pi (√(61))^2 = 61\pi`