Conditional statement is a statement with a hypotesis and a conclusion:
If
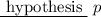 , then
, then
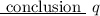 or mathematically
or mathematically
 .
.
Converse statement of
 is statement
is statement
 .
.
If you negate (that means stick a "not" in front of) both the hypothesis and conclusion, you get the inverse:
 .
.
Finally, if you negate everything and flip p and q (taking the inverse of the converse) then you get the contrapositive:
 .
.
Then,
Answer: the correct choice is D (the inverse of the original conditional statement).