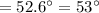Question

A vertical pole 6 feet long casts a shadow 55 inches long. Find the angle of elevation of the sun. Draw a diagram and find the angle of elevation of the sun.

A.) 6.2°

B.) 37.4°

C.) 53.0°

Answer 1

Length of the pole is = 6 feet=6*12=72 inches

Length of shadow of the pole = 55 inches

Here we use tangent function which relates height and shadow . Let the angle of elevation be x .

`tan x = (height)/(shadow)`

`tan x = (72)/(55)`

x= 52.6 degree= approx 53 degree

So the correct option is C.

Answer 2

A vertical pole(AB) 6 feet long casts a shadow(CB) 55 inches long as shown in the attached image. Since the angle of elevation of sun is
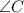`\angle C`. We hav to find the value of
`\angle C`.

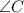Firstly, we will change the dimensions of pole(in feet) to the dimension of shadow( in inches) . So, that the dimensions of pole and shadow are same.

Since, 1 feet = 12 inches.

6 feet =
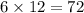`6 * 12 = 72` inches.

Now, let us consider the triangle ABC in the attached image,

We have to find
`\angle C`

`tan\Theta =(Perpendicular)/(base)`

`\tan C`=
`(AB)/(BC)= (72)/(55)`

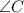
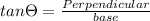
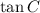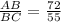
= 1.309

`= 52.6^(\circ) = 53^(\circ)`