Question

Select the following series as arithmetic, geometric, or neither. 3/2 + 3/4 + 3/8 + 3/16 + 3/32

Answer 1

Geometric

Explanation:

Answer 2

Geometric

Explanation:

Given :
`(3)/(2) +(3)/(4) +(3)/(8)+(3)/(16) + (3)/(32)`

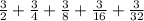
To Find: the following series as arithmetic, geometric, or neither.

Solution:

Find the common difference d .

If difference between the consecutive terms are same . So, the series is arithmetic.

`d=a_2-a_1=(3)/(4)-(3)/(2)=(3-6)/(4)=(-3)/(4)`

`d=a_3-a_3=(3)/(8)-(3)/(4)=(3-6)/(8)=(-3)/(8)`

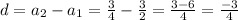
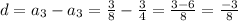
Since the common difference is not same between the two consecutive terms . So, The given series is not arithmetic.

Now find the common ratio r

If the ratio between the two consecutive terms are same than the sequence is geometric.

`r =(a_2)/(a_1)=((3)/(4))/((3)/(2))=(2)/(4)=(1)/(2)`

`r =(a_3)/(a_2)=((3)/(8))/((3)/(4))=(4)/(8)=(1)/(2)`

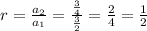
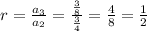
Since the ratio between the consecutive terms are same .

So, The given sequence is G.P.