Answer:
Neither
Explanation:
Given: The given vectors are
 and
and
 .
.
To find: To find whether the vectors u and v are parallel, orthogonal, or neither
Solution: Two vectors are said to be orthogonal if they are perpendicular to each other that is the dot product of the two vectors is zero.
Let us consider the dot product of the vectors
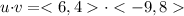

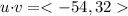
which is not equal to zero.
Hence, the given vectors are not orthogonal.
Two vectors are said to be parallel if one vector is a scalar multiple of the other vector.
In the given vectors, it can be observed that , one vector can not be expressed as the scalar multiple of the other vector.
Hence, the given vectors are neither parallel nor orthogonal.