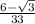Question

What is the answer for:
1÷6 + √3

Answer 1

1.89871747424 heres the answer

Answer 2

To simplify the given expression we need to remove the radical from the denominator by rationalizing it.

To rationalize a radical expression first step is multiply both numerator and denominator of the expression by the conjugate of it's denominator.

So, conjugate of 6+√3 = 6-√3.

Hence,

`(1)/(6+√(3)) *(6-√(3))/(6-√(3))`

=
`(6-√(3))/((6+√(3))(6-√(3)))`

=
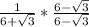
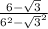`(6-√(3))/(6^2-√(3)^2)` Since (a+b)(a-b)= a^2-b^2

=
`(6-√(3))/(36-3)`

=
`(6-√(3))/(33)`

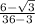
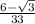
So, the answer is
`(6-√(3))/(33)`