Question

Let's say you were depositing money in the bank. You're going to deposit money every day for a year. The first day you deposit $5, the second day $15 and the third day $25. Then you start wondering how much money you'll be depositing on the 300th day of the year. What equation would you use to answer this question?

Answer 1

$2995 on 300th

Explanation:

Answer 2

First day deposited amount = $5

Second day deposited amount = $15

Third day deposited amount = $25

we see that 5, 15, 25, ... form Arithmetic progression so we can use properties of arithmetic progression to calculate the answer.

300th day deposite value will be given by nth term formula which is

`a_n = a_1 +(n-1)d`

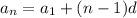
Where a1=first term = 5

n=300 th term

d= common difference = 15-5 = 10

Now plug these values into above formula

`a_(300) = 5 +(300-1)*10`

`a_(300) = 5 +299*10`

`a_(300) = 5 +2990`

`a_(300) = 2995`

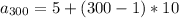
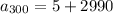
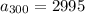
So you will deposit $2995 on 300th day of the year. and the equation used will be
`a_(n) = 5 +(n-1)*10`

where n represents number of day.