Question

A segment has endpoints A (-1, 1) and B (8, 4) . If the segment is divided into four equal parts, the coordinates of the point closest to point A are _____. (7/2, 5/2) (5/4, 7/4) (23/4, 13/4)

Answer 1

ANSWER IS ( 5/4 , 7/4 ).

Explanation:

Answer 2

Line is divided into 4 equal parts.

we have to find a point which is closest to point A.

So that means required point P(x,y) is at 1 unit away from A(-1,1) and 3 unit away from B(8,4)

Now we just need to use section formula to get the coordinate of required point using m1=1 and m2=3

`\left ( (m_1x_2+m_2x_1)/(m_1+m_2) , (m_1y_2+m_2y_1)/(m_1+m_2) \right )`

`= \left ( (1*8+3*(-1))/(1+3) , (1*4+3*1)/(1+3) \right )`

`= \left ( (8-3)/(4) , (4+3)/(4) \right )`

`= \left ( (5)/(4) , (7)/(4) \right )`

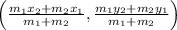
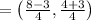
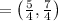
So the final answer is
`\left ( (5)/(4) , (7)/(4) \right )`.