Answer:
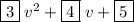
Explanation:
Original expression: 3 + v + 4v² + 2 - v² +3v
Combining like terms in a equation means grouping them together to get a single instance of that term instead of multiple
For example in this expression we can see there is a +4v² and a -v². Group these together and simplify algebraically to get a single v² expression. Do the same with the others.
3 + v + 4v² + 2 - v² +3v
Group the v² terms together to get 4v² - v² = 4v² - 1v² = 3v² (v² == 1v²)
(since the variables are same we can simply add the coefficients
Now group the v terms and simplify
3 + v + 4v² + 2 - v² + 3v
v + 3v = 4v
Finally group the constants
3 + v + 4v² + 2 - v² +3v
3 + 2 = 5
So the final expression is
3v² + 4v + 5
The numbers are what you put in the boxes for each
Usually this process is done in a few steps
3 + v + 4v² + 2 - v² +3v
= (4v² - v²) + (v + 3v) + (3 +2)
= 3v² + 4v + 5