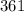Question

What is the sum of 2n-1 from 1-19 in geometric sequence?

Answer 1

For the given sequence 2n-1,

Let n=1 , so the first term of the sequence =
`(2 * 1) -1 =1`

For n=2, the second term of the sequence=
`(2 * 2) -1 =3`

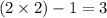
For n =3, the third term of the sequence =
`=(2 * 3) -1 =5`

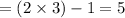
Similarly, for n= 19, the last term of the sequence =
`(2 * 19) -1 =37`

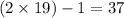
Therefore, the sequence is
`1,3,5,7,....37`

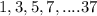
Since the common difference of the sequence formed is 2 which is same throughout the sequence. Hence, it forms an arithmetic progression.

Sum of arithmetic progression is given by =
`(n)/(2)(a+l)`

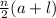
where 'a' is the first term and 'l' is the last term of the given sequence.

Sum=
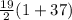
`(19)/(2)(1+37)`

=
`361`