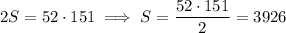Suppose
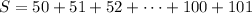
At the same time, we can write
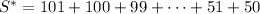
Note that
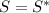 (just reverse the sum). Let's pair the first terms of
(just reverse the sum). Let's pair the first terms of
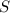 and
and
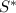 , and the second, and the third, and so on:
, and the second, and the third, and so on:
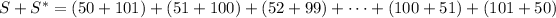
Now, each grouped term in the sum on the right side adds to 151. There are 52 grouped terms on that same side (because there are 50 numbers in the range of integers 51-100, plus 50 and 101), which menas
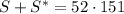
But
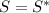 , as we pointed out, so
, as we pointed out, so