Answer:
You pick the second option.
Your salary at the end of the first month will be $10,737,418.23
Explanation:
Option 1:
$5000 for the next two months.
Option 2:
A geometric sequence, with common ratio r = 2.
The common ratio of a geometric sequence is the division of the term
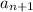 by the term
by the term
 .
.
Here, the geometric sequence is {0.01, 0.02, 0.04,....}, since a penny is 1 cent.
The sum of the first n terms of a geometric sequence is given by the following formula:
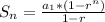
In which
 is the first term, so
is the first term, so
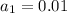 .
.
For the next two months, so 60 days.
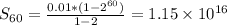
This is higher than $5,000, so you pick the second option.
How much will your salary be at the end of the first month?

Your salary at the end of the first month will be $10,737,418.23