Question

The area enclosed by the curve y^2 = x(1 − x) is given by

Answer 1

`y^2 = x(1-x) = x- x^2`

`x^2 + y^2 = x`

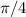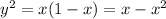
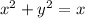
That's a circle, as we can see by the usual completing of the square,

`x^2 - x + y^2 = 0`

`x^2 - x + \frac 1 4 + y^2 = \frac 1 4`

`(x - \frac 1 2)^2 + y^2 = (\frac 1 2 )^2`

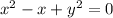
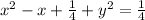
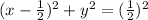
That's the circle of radius
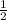`\frac 1 2` centered at
`(\frac 1 2, 0)`

It's a pretty good substitute for the unit circle with some interesting trigonometry of its own.

Anyway its radius is a half so its area is
`\pi r^2 = \pi (\frac 1 2 )^2 = (\pi)/(4)`

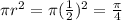
Answer:
`\quad \pi / 4`