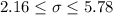Question

Assume that the heights of men are normally distributed. a random sample of 16 men have a mean height of 67.5 inches and a standard deviation of 3.2 inches. construct a 99% confidence interval for the population standard deviation, σ.

Answer 1

Answer:
`2.16\leq\sigma\leq5.78`

Explanation:

The confidence interval for population standard deviation is given by :-

`\sqrt{((n-1)s^2)/(\chi^2_(\alpha/2))}<\sigma<\sqrt{((n-1)s^2)/(\chi^2_(1-\alpha/2))}`

Given : n = 16

Standard deviation : s = 3.2

Significance level :
`\alpha: 1-0.99=0.01`

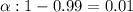
Critical values by using chi-square distribution table :-

`\chi^2_(n-1, \alpha/2)}=\chi^2_(15, 0.005)}=32.80`

`\chi^2_(n-1, 1-\alpha/2)}=\chi^2_(15, 0.995)}=4.6`

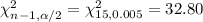
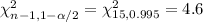
The 99% confidence interval for the population standard deviation is given by :-

`\sqrt{((15)(3.2)^2)/(32.80)}\leq\sigma\leq\sqrt{((15)(3.2)^2)/(4.6)}\\\\\approx2.16\leq\sigma\leq5.78`

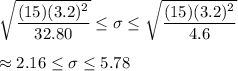
Hence, a 99% confidence interval for the population standard deviation :
`2.16\leq\sigma\leq5.78`

Answer 2

Solution: The 99% confidence interval for the population standard deviation is given below:

`\sqrt{\frac{(n-1)s^(2)}{chi^(2)_{(\alpha)/(2)}}} \leq`σ
`\leq \sqrt{\frac{(n-1)s^(2)}{chi^(2)_{1-(\alpha)/(2)}}}`

`\sqrt{(15 (3.2)^(2))/(30.578)}\leq`σ
`\leq \sqrt{(15(3.2)^(2))/(4.601)}`

`2.2\leq`σ
`image`