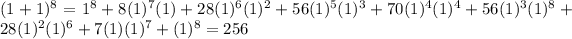Question

Explain why it would not make sense to approximate 256 using the binomial theorem for the binomial (20 + 5)6.

Answer 1

Because 5 is not between -1 and 1, when it is raised to a positive integer exponent it will not approach 0. Therefore, all seven terms would need to be calculated and added to find (20 + 5)6

Answer 2

The formula for the Binomial Theorem with a power 6 is as:

`(x+y)^6=x^6+6x^5y+15x^4y^2+20x^3y^3+15x^2y^4+6xy^5+y^6`

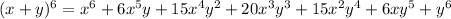
Thus, if we plug in 20 for x and 5 for y, our first term itself will be
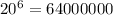`20^6=64000000` which is much greater than 256 and thus it will not make any sense to use
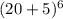`(20+5)^6` to approximate 256 using the binomial theorem.

Also, it will not make any sense to use
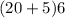`(20+5)6` as that has no power and we know that Binomial Theorem makes use of Power. Anyway,
`(20+5)6=150\\eq 256`.

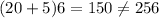Our best bet here would be to use the equation with power 8:

`(x+y)^8=x^8+8x^7y+28x^6y^2+56x^5y^3+70x^4y^4+56x^3y^8+28x^2y^6+7xy^7+y^8`

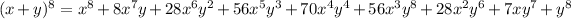
and have
`x=1` and
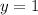`y=1` which will give us

`(1+1)^8=1^8+8(1)^7(1)+28(1)^6(1)^2+56(1)^5(1)^3+70(1)^4(1)^4+56(1)^3(1)^8+28(1)^2(1)^6+7(1)(1)^7+(1)^8 =256`