Question

The number of column inches of classified advertisements appearing on mondays in a certain daily newspaper is normally distributed with population mean of 320 and population standard deviation of 20 inches. referring to scenario 6-1, for a randomly chosen monday, what is the probability there will be less than 340 column inches of classified advertisement? question 5 options:

Answer 1

Let X be the number of column inches of classified advertisements appearing on mondays in a certain daily newspaper.

X follows Normal distribution with mean μ =320 and standard deviation σ=20

The probability that there will be less than 340 column inches of classified advertisement

P(x < 340 ) =
`P( (x - mean)/(standard deviation) < (340 - 320)/(20) )`

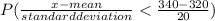
= P(z < 1)

Using z score table to find probability below z=1 is

P(z< 1) = 0.8413

P(x < 340 ) = P(z<1) = 0.8413

The probability there will be less than 340 column inches of classified advertisement is 0.8413

Answer 2

The sample mean is μ=320, and sample standard deviation is equal to population standard deviation σₓ=20.

The Z-score is
`Z=( 340-320)/(20)=1`.

Refer to standard normal distribution table.

The required probability is

`P(X<340)=P(Z<1)=<strong>0.8413</strong>`