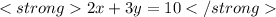Question

If 8x^3 + 27y^3 = 730 and 3x^2y + 3xy^2 = 15 then evaluate 2x + 3y
Pls help me

Answer 1

Given that, "
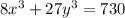`\\8x^3 + 27y^3 = 730` and
`3x^2y + 3xy^2 = 15`"

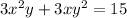Using this two equations evaluate
`2x+3y`:

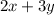Using Cube formula for a+b,

`(a + b)^3 = a^3 + b^3+3a^2b + 3ab^2`

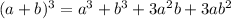
Plug in a=2x \,\, \, and\, \, \, b=3y in the formula,

`(2x+3y)^3=(2x)^3+(3y)^3+3* (2x)^2* (3y)+3* (2x)* (3y)^2`

`=8x^3+27y^3+36x^2y+54xy^2`

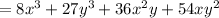
We know that the value of
`8x^3 + 27y^3 = 730`

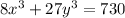
Plug in this value in the above equation,

`(2x+3y)^3=730+36x^2y+54xy^2`

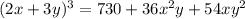
Now take 18 as common for the second and third term in the right hand side,

`(2x+3y)^3=730+18(2x^2y+3xy^2)`

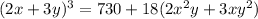
Now plug in the value 2x^2y+3xy^2\: \: as \: \: 15,

`(2x+3y)^3=730+18*15`

`(2x+3y)^3=730+270`

`(2x+3y)^3=1000`

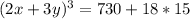
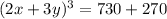
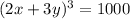
Taking Cube root on both sides, we get

`<strong>2x+3y=10</strong>`