The equation for the height of the rocket at time t given
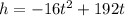
We have to find the time t, when the rocket reaches 560 feet.
That means we have to find t when h = 560 ft. we will place 560 in the place of h to find t now.
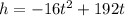
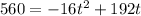
In the right side, we can check -16 is the common factor. So we will take out -16 from the rigbht side.
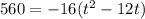
To get rid of -16 from the right side and move it to left side, we will divide both sides by -16.
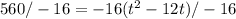

Now we will move -35 to the righ side by adding 35 to both sides.
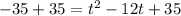
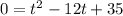
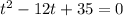
We will factorize thee left side to find the values of t now. We need to find a pair of factors of 35 that by adding them we will get -12.
The pair of factors of 35 are -5 and -7 and by adding -5-7 we will get -12.
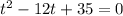
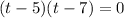
So by using zero product property we will get
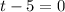
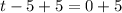

Also
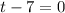
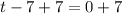

So we have got the rocket reaches at 560ft when t = 5 seconds and also when t = 7 seconds.
Now part b.
When the rocket completes its trajectory and hits the ground then the height or h = 0. So we will place h = 0 there in the equation.
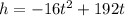
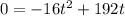
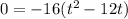
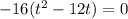
We will move -16 to the other side by dividing it to both sides.
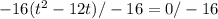
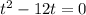
We will take out the common factor t from the left side. By taking out t we will get,
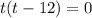
We will use zero product property now. By using that we will get,
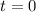
ans also
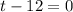
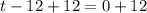

When the rocket completes its trajectory and hits the ground the time t can not be 0. When t =0, the rocket starts the trajectory.
So when the rocket completes its trajectory and hits the ground ,
then t = 12seconds.
So we have got the required answers.