Question

Determine if the vectors v1 = (2, −1, 2, 3), v2 = (1, 2, 5, −1), v3 = (7, −1, 5, 8) are linearly independent vectors in r4 .

Answer 1

Vectors are linearly independent if there doesn't exist a non-trivial linear combination which returns the zero vector. So, we must see if we can find three coefficients
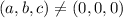`(a,b,c)\\eq(0,0,0)` such that

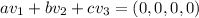`av_1+bv_2+cv_3 = (0,0,0,0)`. We have

`av_1 = (2a, -a, 2a, 3a)`

`bv_2 = (b, 2b, 5b, -b)`

`cv_3 = (7c, -c, 5c, 8c)`

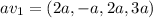
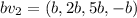
So,
`av_1+bv_2+cv_3 = (2a+b+7c, -a+2b-c, 2a+5b+5c, 3a-b+8c)`

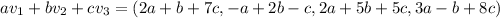
This linear combination returns the zero vector if

`2a+b+7c = 0`

`-a+2b-c = 0`

`2a+5b+5c = 0`

`3a-b+8c = 0`

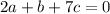
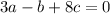
This system admits the only trivial solution a=b=c=0, so the vectors are linearly independent.