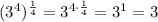If I understood coorectly, you're looking for the fourth root of 81. This exercise can be solved by remembering that extracting the fourth root of a number is the same as raising that number to the power of 1/4.
We also need the prime factorization of 81, which is
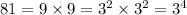
So, the fourth root of 81 is 81 raised to the power of 1/4, which means
![\sqrt[4]{81} = \sqrt[4]{3^4} = (3^4)^{(1)/(4)}](https://img.qammunity.org/2019/formulas/mathematics/high-school/n2gxov6qa3b8c8t90i23dfvyrz5wbl77q3.png)
Now, use the property of exponents
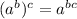 to convert the expression into
to convert the expression into