Question

Which equation describes the same line as y-6 = -4(x+1)

Answer 1

`y=-4x+2`

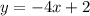
Explanation:

We have been given equation of a line in point slope form. We are supposed to find equation of the same line in another form.

We will convert our given equation in slope-intercept form.

`y-6=-4(x+1)`

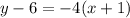
Using distributive property
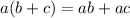`a(b+c)=ab+ac`, we will get:

`y-6=-4*x-4*1`

`y-6=-4x-4`

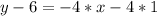
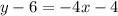
Now, we will add 6 on both sides of our equation.

`y-6+6=-4x-4+6`

`y=-4x+2`

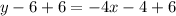
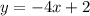
Therefore, our required equation would be
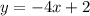`y=-4x+2`.

Answer 2

Distribute -4 to all terms within the parenthesis

-4(x + 1) = -4x -4

y - 6 = -4x - 4

Isolate the y. Add 6 to both sides

y - 6 (+6) = -4x - 4 (+6)

y = -4x - 4 + 6

Combine like terms

y = -4x (-4 + 6)

y = -4x + 2

y = -4x + 2 is your equation.

hope this helps