Q1.
f(x)=2.5x - 10.5
f(2)=2.5(2)-10.5 = -5.5
They'll go up by 2.5 from here:
x 2 3 4 5 6
f -5.5 -3.0 -0.5 2.0 4.5
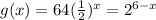

Each subsequent x halves the value. Our table is now
x 2 3 4 5 6
f -5.5 -3.0 -0.5 2.0 4.5
g 16 8 4 2 1
We see they intersect at x=5
Answer: x=5
Check:
f(5) = 2.5(5) - 10.5 = 2
g(5) = 64(.5)^5 = 64/32=2 good
Q2.
The total revenue is really the area under those two lines. For print ads that's a trapezoid,
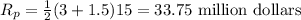
For online ads it's a triangle:
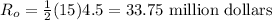
Those are estimated to be exactly the same, so the marketing executive was exaggerating when they said since started the revenue from online is double that from print. A lying marketing exec, imagine that.
They could have truthfully said that currently the revenue from online ads is triple that from print ads, and that trend is increasing.
Answer: It looks like around t=7.5, somewhere in the seventh year, the revenues were equal.
Q3.
A. Just looking at the data evenly spaced every five years,
Year 0 5 10 15
West 100 90 80 70
Dunes 20 45 70 95
These each have a common first difference.
For Western we see a decrease of 10 feet every five years, a slope of -2.
For Dunes we see an increase of 25 feet every five years, a slope of 5.
The y intercepts are the initial values so as equations,
w(t) = -2 t + 100
d(t) = 5t + 20
From the graph we see t between 11 and 12 is the meet. Let's solve the equation.
-2t + 100 = 5t + 20
80 = 7 t
t = 80/7 = 11.4...
Answer part B: between years 11 and 12
Answer part C: solve the equation like we did