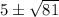Answer:
Option 2nd is correct
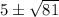
Explanation:
Given the equation:
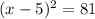
Taking square root both sides we have;
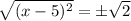
Using the exponent rule:
![\sqrt[n]{x^n}=x](https://img.qammunity.org/2019/formulas/mathematics/high-school/ta48snlpv13oqqjhovwm7wsf0fu6mnopcg.png)
then;
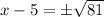
Add 5 to both sides we have;
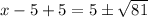
Simplify:
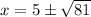
Therefore, the following expressions represents the solutions to the given equation is,