Question

A deck of 52 cards has 4 aces. assume you give 13 cards to each of the 4 players. what is the probability that each player gets exactly one ace

Answer 1

Each player gets 13 cards. Total number of ways to get 13 cards by each player is
`C_(52)^(13)\cdot C_(39)^(13)\cdot C_(26)^(13)\cdot C_(13)^(13)`.

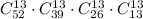In a draw of 13 cards from a deck having 4 aces and 48 non-aces, player 1 must get exactly 1 ace, the number of ways to do this is
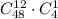`C_(48)^(12)\cdot C_(4)^(1)`. Now to player 2 we deal 13 cards from a deck having 3 aces and 36 non-aces, and player 2 must get exactly 1 ace and ways to do this are
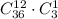`C_(36)^(12)\cdot C_3^1`. Then we deal 13 cards to player 3 from a deck having 2 aces and 24 non-aces, and player 3 must get exactly 1 ace with number of ways to do this
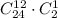`C_(24)^(12)\cdot C_2^1`. If players 1-3 each have exactly 1 ace we are done: player 4 will also get one ace. Use the product rule to calculate total number of ways:
`C_(48)^(12)\cdot C_(4)^(1)\cdot C_(36)^(12)\cdot C_3^1\cdot C_(24)^(12)\cdot C_2^1`.

The probability is
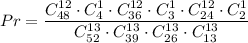`Pr=(C_(48)^(12)\cdot C_(4)^(1)\cdot C_(36)^(12)\cdot C_3^1\cdot C_(24)^(12)\cdot C_2^1)/(C_(52)^(13)\cdot C_(39)^(13)\cdot C_(26)^(13)\cdot C_(13)^(13))`.