Question

Why is MAE TON? HL HA LL

Answer 1

if the Hypotenuse and Leg of a right-triangle are congruent to corresponding parts of another right-triangle, then the triangles are congruent by HL.

HL theorem.

Answer 2

1. HL: Hypotenuse-leg theorem.

Step by step explanation:

We have been given two right triangles and we are asked to find how our triangles are congruent to each other.

Since we know that if one leg and hypotenuse of a right triangle is congruent to leg and hypotenuse of another triangle then both triangles are congruent. We will use Pythagorean theorem to prove our answer.

In
`\Delta MAE`,
`(AM)^(2) =(AE)^(2) +(EM)^(2)`

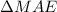In
`\Delta TON`,
`(OT)^(2) =(ON)^(2) +(TN)^(2)`

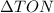We have been given that
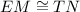`EM\cong TN` and
`AM\cong OT`, so by the definition of congruence EM=TN and AM=OT.

Upon using substitution we will get,

`(ON)^(2)+(TN)^(2) =(AE)^(2) +(EM)^(2)`

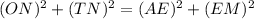
Since we are given that EM=TN,

`(ON)^(2)+(TN)^(2) =(AE)^(2) +(TN)^(2)`

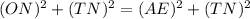
Subtracting
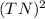`(TN)^(2)` from both sides of equation we will get,

`(ON)^(2)=(AE)^(2)`

`ON\cong AE`

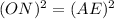
We can see that our angle is congruent by SSS congruence. Therefore, we can see that
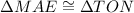`\Delta MAE\cong \Delta TON` by Hypotenuse-leg theorem and first option is the correct choice.