Question

The function g(x) = 8(4x) is reflected across the x-axis to create f(x).

What is the equation for f(x)?

f(x) = _________ (4)^x

Answer 1

`f(x) = -8(4)^x`

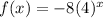
Explanation:

We have been given the equation of g(x) is
`g(x)=8(4)^x`

When we reflect a function f(x) about the x-axis then the equation of function becomes -f(x).

Now, f(x) is created by reflecting across the function g(x) about x axis. Hence, we have

f(x) = -g(x)

`f(x) = -8(4)^x`

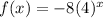
Thus, we can fill -8 in the blank provided.

Answer 2

to reflect across the x axis , we multiply the function by negative

So the function reflected across the x axis should be

`f(x) = -8 (4)^x`

f(x) = ____-8_____ (4)^x