Question

The variable z is inversely proportional to x. When x is 19, z has the value 0.10526315789474. What is the value of z when x= 28? Round to at least the thousandths place if needed.

Answer 1

When two variables are inversely proportional the relation between them can be written as:

`z=(k)/(x)`

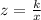
Here, k is the constant of proportionality and is always equal to the product of the two variables. So using the given values of z and x, we can find k first.

`image`

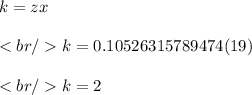
The constant of proportionality for the given inverse proportion comes out to be 2. Using the value of k in the equation, we get:

`z=(2)/(x)`

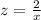
We have to find the value of z when x=28. So replacing x by 28, we get:

`image`

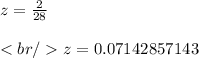
Thus, rounding of to nearest thousand the value of z comes out to be 0.071 if x is equal to 28.