Question

1. The value of ^3√626 is between which two integers?

a. between 5 and 6


b. between 7 and 8


c. between 8 and 9


d. between 9 and 10



2. The value of √52 is between which two integers?


a. between 7 and 8


b. between 8 and 9


c. between 6 and 7


d. between 5 and 6



3. Select the expression equal to √44


a. 2√11


b. 4√11


c. 11√4


d. 2√22



4. Select the expression equal to ^3√108


a. 6


b. 3^3√3


c. 4^3√3


d. 3^3√4

Answer 1

First question:

The cube root of 626 is a number than, when cubed, returns 626. So, if it is between two integers n and n+1, it means that
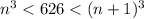`n^3 < 626 < (n+1)^3`. This is the case for 8 and 9, since you have
`8^3 = 512 < 626 < 729 = 9^3`.

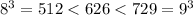Second question:

The square root of 52 follows the same principles of the first question, but you have to square the numbers instead of cubing them. So, this time the number lies between 7 and 8, since
`7^2 = 49 < 52 < 64 = 8^2`.

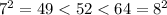Third question:

To solve this kind of exercises, factor the number under the root, and use the root property
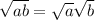`√(ab)=√(a)√(b)`. You have

`√(44) = √(4\cdot 11) = √(4)√(11) = 2√(11)`

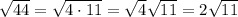
Fourth question:

This exercise is similar to the third one, but again you change the order of the root. So, you have

`\sqrt[3]{108} = \sqrt[3]{2^23^3} = 3\sqrt[3]{4}`