Do the angles say nice things to each other or do they add to ninety degrees? Complimentary or complementary?
It's not really the minimum, it's the smaller maximum.
Enough correcting the question; let's answer it.
We have
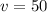 meters/sec. We're only interested in the y component of velocity.
meters/sec. We're only interested in the y component of velocity.
If the first has

then the second is
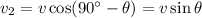
We get a maximum when the velocity is zero, so for the first
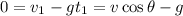
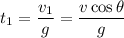
corresponding to a maximum height
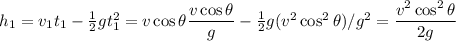
So
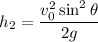
We're given


That's the double angle formula but we'll avoid being tempted.

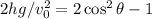
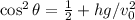
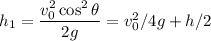
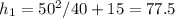
Choice 2