Question

If -3 + i is a root of the polynomial function f(x), what can also be a root of f(x)?

Answer 1

Polynomials of degree n are linear combination of powers of a variable, i.e. they are the sum of all the powers of the variable from 0 to n, with some coefficients. So, a generic polynomial of degree n is written as

`a_nx^n+a_(n-1)x^(n-1)+...+a_2x^2+a_1x+a_0`

The fundamental theorem of algebra states that a polynomial of degree n has exactly n roots.

Moreover, polynomials with real coefficients also have the following property: if
`\alpha \in \mathbb{C}` is a solution of a polynomial, its conjugate
`\overline{\alpha}` is also a solution of the same polynomial.

The conjugate is obtained by changing the sign of the complex part of the number:

`\alpha = a+bi \to \overline{\alpha} = a-bi`

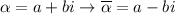
So, if
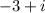`-3+i` is a solution of the polynomial also its conjugate
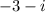`-3-i` is a solution of the polynomial