Question

Farmer ed has 700 meters of​ fencing, and wants to enclose a rectangular plot that borders on a river. if farmer ed does not fence the side along the​ river, find the length and width of the plot that will maximize the area. what is the largest area that can be​ enclosed?

Answer 1

Length = 350 meters

Width = 125 metres

Maximum area = 43750 meter²

Explanation:

Farmer Ed has total fencing = 700 meters

Let the length of rectangular plot is = x meters

Let the width of the plot is = y meters

Since fencing is to be done on three sides so x + 2y = 600 -------(1)

Now the area of plot A = xy --------(2)

Now we substitute the value of x in the equation 2 from equation 1.

A = y(600 - 2y)

A = 600y - 2y²

For the maximum area we find the derivative of the plot which will be equal to the zero.

`(dA)/(dy)=(d)/(dy) (600y-2y^(2))`

= 600 - 4y

`(dA)/(dy)=0`

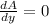
600 - 4y = 0

4y = 600

y = 125 meters

By putting y = 125 in equation 1

x + 2(125) = 600

x + 250 = 600

x = 600 - 250

x = 350 meters

So the length will be 350 meters and width will be 125 meters

And the largest area enclosed will be = 350×125 = 43750 meter²