Question

Suppose an object’s initial velocity is 10 m/s and its final velocity is 4 m/s. Mass is constant.

What can best be concluded about the object based on the work-energy theorem?

Work is positive, the environment did work on the object, and the energy of the system increases.
Work is positive, the object did work on the environment, and the energy of the system increases.
Work is negative, the object did work on the environment, and the energy of the system decreases.
Work is negative, the environment did work on the object, and the energy of the system decreases.

Answer 1

Its C I just did it on edge

Answer 2

The correct answer is:

Work is negative, the environment did work on the object, and the energy of the system decreases.

In fact, the work-energy theorem states that the work done by the system is equal to its variation of kinetic energy:

`W=\Delta K=K_f -K_i`

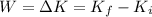
In this problem, the variation of kinetic energy
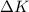`\Delta K` is negative (because the final velocity is less than the initial velocity), so the work is negative, and this means that the environment did work on the object, and its energy decreased.