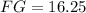Question

URGENT HELP NEEDED WITH RIGHT TRIANGLES! (MULTIPLE PROBLEMS)!!! Please give an in depth explanation :D

Answer 1

Remember "SOH CAH TOA"

Sine = (Opposite/Hypotenuse)

Cosine = (Adjacent/Hypotenuse)

Tangent = (Opposite/Adjacent)

1st Problem:

Remember that cosine is (Adjacent/Hypotenuse). And also know that we are using inverse trig (regular trig solves for sides, inverse solves for angles.)

`cos^(-1)((17)/(24)) =44.9005`

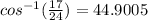
2nd Problem:

For this we are using Cosine (Adjacent/Hypotenuse) to solve for the adjacent side. Your equation will look like this:
`(cos(49))/(1) =(x)/(10)`

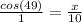
For this, all you need to do is cross multiply, and your answer will be
`6.6=x`

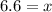
3rd Problem:

So this is actually a special triangle. Because its an isosceles right triangle, it follows the 45-45-90 rule, which is if one of the legs is x, then the other leg is also x and the hypotenuse is x√2.

In this case, EF is going to be 16√2, or 22.63 cm, because 1. for the hypotenuse to not have √2 means that the leg does. Remember that √2(√2) = 2, which means that we would need to know what times 2 makes 32, which is 16.

4th Problem:

So for this we will be using the pythagorean theorem, which is
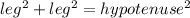`leg^2+leg^2=hypotenuse^2` . In this case, the equation is going to be
`15^2+19^2=GH^2`

Firstly, solve the exponents:
`225+361=GH^2`

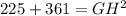
Next, combine 225 and 361 together:
`586=GH^2`

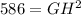
Lastly, square root each side, and your answer should be
`24.2=GH`

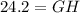
5th Problem:

So you'll be using the pythagorean theorem like before, except with new numbers and your solving for one of the legs.

`19^2+FG^2=25^2`

Like before, solve the exponents:
`361+FG^2=625`

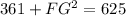
Next, subtract 361 on both sides:
`FG^2=264`

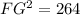
Lastly, square root both sides, and your answer should be
`FG=16.25`