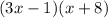Question

PLEASE HELP!

What are the factors of 3x2 + 23x − 8?
(3x − 4)(x + 2)
(3x − 2)(x + 4)
(3x − 8)(x + 1)
(3x − 1)(x + 8)

Answer 1

Option (d) is correct.

The factored form of given quadratic equation
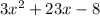`3x^2+23x-8` is
`(3x-1)(x+8)`

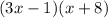
Explanation:

Given :equation
`3x^2+23x-8`

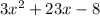
We have to factorize the given quadratic equation.

Consider the given quadratic equation
`3x^2+23x-8`

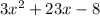
we can factorize the given quadratic equation using middle term splitting method,

split middle term in such a way that the middle term becomes the product of two other terms.

23x can be written as 24x-x

equation becomes,

`3x^2+23x-8`

`\Rightarrow 3x^2+24x-x-8`

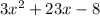
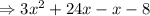
Taking 3x common from first two terms and -1 common from last two terms , we get,

`\Rightarrow 3x(x+8)-1(x+8)`

`\Rightarrow (3x-1)(x+8)`

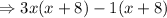
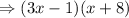
Thus, The factored form of given quadratic equation
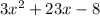`3x^2+23x-8` is
`(3x-1)(x+8)`

Answer 2

`3x^2 + 23x - 8` can be factored into
`(3x - 1)(x + 8)`. To double-check, you can multiply the terms together again using FOIL: first, outside, inside, last.

(3x)(x) + (3x)(8) + (-1)(x) + (-1)(8)

3x² + 24x - x - 8

3x² + 23x - 8

Check.