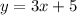Question

SOMEONE HELP OUT I DONT HAVE MUCH TIME

Answer 1

To solve this problem you must apply the proccedure shown below:

1. If both lines are parallel, they have the same slope (
`m=3`)

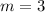2. You have that the equation of the line is:

`y=mx+b`

Where
`m` is the slope and
`b` is the y-intercept.

3. You know that the other line must pass through the point (
`1,8`). So, you can solve for
`b` to calculate its value, as following:

`8=3(1)+b\\ b=5`

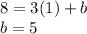
4. Therefore, the equation of the line that is parallel to
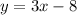`y=3x-8` is

`y=3x+5`

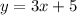
The answer is:
`y=3x+5`