Question

Which equation is y=-6^2+3x+2 rewritten in vertex form?

Answer 1

Answer: The correct option is

(C)
`y=-6\left(x-(1)/(4)\right)^2+(19)/(8).`

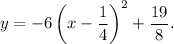
Step-by-step explanation: We are given to select the equation that is the vertex form of he following equation :

`y=-6x^2+3x+2~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

We know that

the vertex form of a function y = f(x) is written as

`y=a(x-h)^2+k,` where (h, k) is the vertex.

From equation (i), we have

`y=-6x^2+3x+2\\\\\\\Rightarrow y=-6\left(x^2-(1)/(2)x\right)+2\\\\\\\Rightarrow y=-6\left(x^2-2* x*(1)/(4)+\left((1)/(4)\right)^2\right)+2+6* \left((1)/(4)\right)^2\\\\\\\Rightarrow y=-6\left(x-(1)/(4)\right)^2+2+(6)/(16)\\\\\\\Rightarrow y=-6\left(x-(1)/(4)\right)^2+2+(3)/(8)\\\\\\\Rightarrow y=-6\left(x-(1)/(4)\right)^2+(16+3)/(8)\\\\\\\Rightarrow y=-6\left(x-(1)/(4)\right)^2+(19)/(8).`

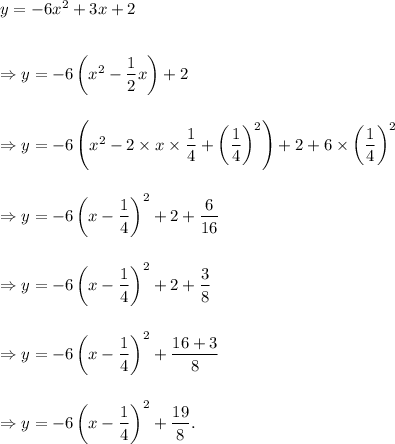
Thus, the required vertex form of the given equation is

`y=-6\left(x-(1)/(4)\right)^2+(19)/(8).`

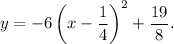
Option (C) is CORRECT.