Question

The value of an antique plate after x years can be modeled by f(x) = 18(1.05)x. Which graph can be used to approximate the number of years it will take for the plate’s value to be $30?

Answer 1

we have that

`f(x)=18*(1.05^(x) )`

using a graph tool

see the attached figure N 1

for f(x)=$30

the number of years x is equal

x=10.47 years

the answer in the attached figure N 2

Answer 2

Option A

Explanation:

Given : The value of an antique plate after x years can be modeled by

`f(x) = 18(1.05)^x`

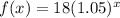
To find : Which graph can be used to approximate the number of years it will take for the plate’s value to be $30.

Solution: First we find the value of x at y=30

`f(x) = 18(1.05)^x`

`30 = 18(1.05)^x`

`(30)/(18)=(1.05)^x`

`1.6666=(1.05)^x`

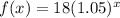
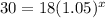
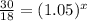
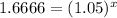
Taking log both side and apply property
`logx^a=alogx`

`log(1.6666)=xlog(1.05)`

`0.221848749616=x0.0211892990699`

`(0.221848749616)/(0.0211892990699)=x`

`x=10.4698484308`

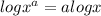
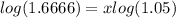
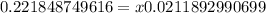
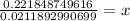
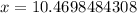
Therefore, from the given graph where the value (x,y)=(10.47,30) lie and the curve from (0,18) to (10.47,30) is the solution of the answer.

Hence, option A is correct (also correct graph is attached)