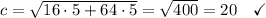Question

The altitude drawn to the hypotenuse of a right triangle divides the hypotenuse into segments such as their lengths are in ratio of 1:4. If the length of the altitude is 8, find the length of: (a) Each segment of the hypotenuse (b) The longer leg of the triangle.

Answer 1

I happen to know that when the foot F of the altitude divides the hypotenuse into two lengths
`d` and
`e`, the altitude
`h` is the geometric mean of
`d` and
`e`, that is
`h^2= de.`

But you probably didn't know that. We'll take our triangle labeled the usual way, right angle C, hypotenuse
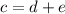`c = d + e`. There are three right triangles, which I'll write without the benefit of the figure. Let's say sides
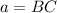`a=BC` and
`d=BF` so

`d^2 + h^2 = a^2`

`e^2 + h^2 = b^2`

`a^2 + b^2 = c^2 = (d + e)^2 = d^2 + 2de + e^2`

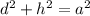
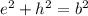
Adding all three equations lots of stuff cancels,

`2h^2 = 2de`

`h^2 = de`

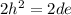
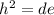
That proves the geometric mean thing. In our problem we have
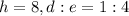`h=8, d:e=1:4` which just means
`e=4d`.

`8^2 = d(4d) = 4d^2`

`d=4`

`e=16`

`b^2=e^2+h^2= 16^2+8^2=5(8^2)`

`b=8√(5)`

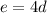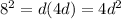
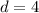
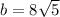
Part a)
`d=4,e=16`

Part b)
`b=8\sqrt 5`

Check:

`a^2=d^2+h^2=16+64=80=16\cdot 5`

The triangle is
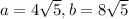`a=4√(5), b=8√(5)` so
`c=√(16\cdot 5 + 64\cdot 5)=√(400)=20 \quad\checkmark`