Question

If you place a 100-foot ladder against the top of a 96-foot building, how many feet will the bottom of the ladder be from the bottom of the building?

Answer 1

x^2+y^2=z^2

x^2+96^2=100^2

x=sqrt(100^2-96^2)

x=28 so the distance from the base of the ladder and the base of the ladder is 28ft.

Hope this helps. Any questions please just ask. Thank you.

Answer 2

28 ft

Explanation:

I add a graph to this question.

In the graph we can see that the ladder, the building and the distance ''x'' form a right triangle.

We can use the Pythagorean theorem to solve this exercise. The Pythagorean theorem states that if ''a'' and ''b'' are the sides of a triangle and 'h'' is its hypotenuse ⇒

`a^(2)+b^(2)=h^(2)`

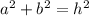
If we apply this equation to the graph we can find the distance ''x'' :

`x^(2)+(96ft)^(2)=(100ft)^(2)`

`x^(2)+9216(ft^(2))=10000(ft^(2))`

`x^(2)=784(ft^(2))`

`x=\sqrt{784(ft^(2))}`

`x=28ft`

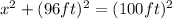
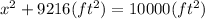
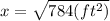
We find that the distance ''x'' is 28 ft