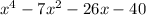Question

Write a polynomial function of minimum degree with real coefficients whose zeros include those listed. Write the polynomial in standard form. 4, -2, and -1 + 2i

Answer 1

This is going to be a fourth degree polynomial because if x = 4, one of the factors is x - 4; if x = -2, then one of the factors is x + 2; and by the conjugate root theorem, if x = -1 + 2i, then -1-2i HAS to also be a root. If x = -1+2i, then the factor is (x-(-1+2i)). Simplfying that gives us (x+1-2i). Likewise, if x = -1-2i, then the factor is (x-(-1-2i)). Simplifying that gives us (x+1+2i). We will FOIL those complex factors first. Doing that we have
`x^2+x-2ix+x+1-2i+2ix+2i-4i^2`. Once we simplify that down it's much easier to deal with than what it looks like right now.
`x^2+2x+1-4i^2`. Since i^2 = -1, what we have in the end is
`x^2+2x+5`. Now we will multiply that by x-4.
`(x^2+2x+5)(x-4)=x^3-2x^2-3x-20`. Now finally we will multiply in the last factor of x+2.
`x^4-7x^2-26x-40` is your final fourth degree polynomial.

Answer 2

`x^(4) - 7x^(2) -26x-40`

Explanation:

The polynomial will be a fourth degree polynomial.

Let's take x = 4, then one of the factors is x - 4.

Then if x = -2, then the factor will be:

x + 2 = -2+ 2

x + 2 = 0

Then one of the polynomials is x + 2

Using the conjugate theorem:

if x = -1 + 2i, then -1-2i will be the root.

Then if x = -1+ 2i, then the factor of the function will be x- 1- 2i

Similarly, if x = -1-2i, then the factor x -(-1-2i)

This gives the final expression:

`x^(4) -7x^(2) -26x-40`