So for these system of equations I'll be using substitution to solve. To be able to do that, however, you'll have to subtract 2x on each side of the first equation to get
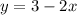
.
Now substitute y in the second equation for (3-2x), and then you can solve for x. Your second equation should look like this:

Multiply -2 and (3-2x) to get

Combine like terms to get

Add 6 on each side to get
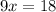
, then divide 9 on each side and your answer should be

Now that we got x, we can just substitute x for 2 in either equation to solve for y.
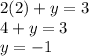 In short, x = 2 and y = -1.
In short, x = 2 and y = -1.