Question

A simple random sample of 49 adults is obtained from a normally distributed population, and each person's red blood cell count has a sample mean of 5.31 and a sample standard deviation of 0.54. use a 0.01 significance level to test the clail that the sample is from a population with a mean less than 5.4, which is a value often used for the upper limit of the range of normal values. what is the critical value?

Answer 1

This is a one sided t test. We need to calculate t, which is the (signed) number of standard deviations the observed average is away from the purported mean. It's a bit odd because here our purported mean is 5.4, which we're told is a really an upper threshold. We'll test if our observed data has an average significantly lower than 5.4.

We have the standard deviation of the individual samples. The standard deviation of the average is the standard deviation of the samples divided by the square root of n. In general,


`t = \frac{\bar{x} - \mu}{ \sigma / √(n) }`


`t = (5.31- 5.4)/( 0.54 / √(49))= -1.67`

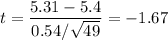
By the 68-95-99.7 rule for a normal distribution this will correspond to a probability of between 2.5% (two sigma) and 16% (one sigma), so not really that close to the 1% significance we were looking for. The probabilities will be even higher for a t distribution than a normal distribution, but n-1=48 degrees of freedom is enough that there won't really be any difference.

Let's look up the values we need in the table.

At 48 dfs (50 really in the table I'm looking at), p=.01 probability corresponds to t=2.4. That's the critical value of t we needed to exceed (in absolute value) for significance.

t=-1.67 at 48 degrees of freedom corresponds to a one sided p=.05, as does the standard normal at z=-1.65, close enough.