Question

Prove that :-
sin 2x + 2 sin 4x + sin 6x = 4 cos² x . sin 4x

Answer 1

Hi there!

L.H.S. = sin 2x + 2 sin 4x + sin 6x

= sin 2x + sin 6x + 2 sin 4x

= 2 sin
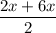
`\frac {2x + 6x}{2}` . cos
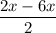
`\frac {2x - 6x}{2}` + 2 sin 4x

= 2 sin 4x . cos (-2x) + 2 sin 4x

= 2 sin 4x . cos 2x + 2 sin 4x

= 2 sin 4x (cos 2x + 1)

= 2 sin 4x (2 cos² x - 1 + 1)

= 2 sin 4x (2 cos² x) = 4 sin 4x . cos² x = R.H.S.

HENCE PROVED.

~ Hope it helps!