Question

A chemistry teacher adds 50.0 ml of 1.50 M H2SO4 solution to 200ml of water . What is the concentration of the final solution?

Answer 1

option A

Step-by-step explanation:

just took test on e2020

Answer 2

When comparing concentration and volume, we can use the equation:


`M_(1) V_(1) = M_(2) V_(2)`

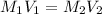
**Note: the volume in this equation is in liters. Be sure to convert mL to L by dividing by 1000.

Now let's plug in the values that were given to us in the equation (using 0.050L for 50 mL and 0.200L for 200 mL):


`(1.50M)(0.050L)= M_(2)(0.200L)`

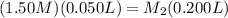
Then we can solve for
`M_(2)`:


`((1.50M)(0.050L))/((0.200L))= M_(2)`


`M_(2)=0.375M`

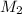
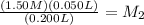
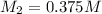
So now we know that the resulting solution has a molarity of 0.375 M.