Let
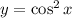
. Then
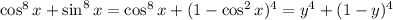
If calculus methods are okay, consider the function
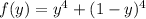
. Then
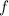
has a critical point where
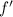
vanishes, i.e.
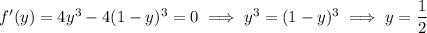
The second derivative
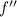
is
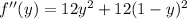
and at this critical point, we have a value of
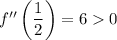
. The derivative test for extrema indicates this is the site of a minimum, and we get a minimum value of
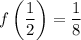
as desired.