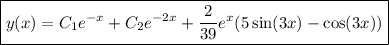Solve the homogeneous equation
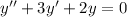
Its characteristic equation is
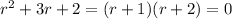
with roots at
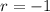 and
and
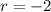 , hence the characteristic solution is
, hence the characteristic solution is
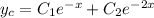
For the nonhomogeneous equation, I'll use variation of parameters. We're looking for a solution of the form
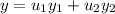
to the equation
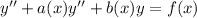
such that
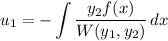
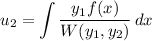
The Wronskian
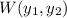 of the two fundamental solutions
of the two fundamental solutions
 and
and
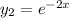 is
is

Then we have
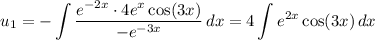
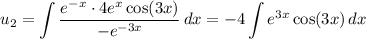
Recall Euler's identity,
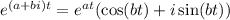
Then we have the general antiderivative
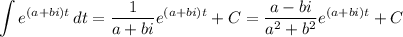
Taking the real parts of both sides, we have
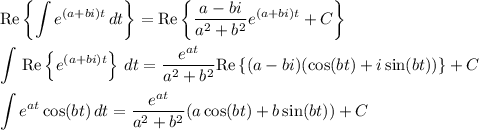
so that
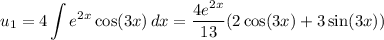
and
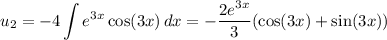
We've found
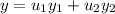
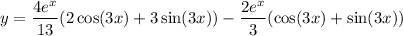

Then the general solution to the differential equation is