Question

A man invested one fifth of his money at 4%, half of his money at 5%, and the rest of his money at 3.5%. If his total annual investment income was $870, how much had he invested? How can I set this up?

Answer 1

namely the interest yield is $870, so all those investments yielded that much after a year.

a = the whole amount he invested.

let's keep in mind that whatever% of anything is just (whatever/100) * anything.

now 1/5 of "a" went with 4%, how much is 1/5 of "a"? well is (1/5)a or a/5.

how much is 4% of a/5? well is just (4/100) * (a/5) or 0.04a/5.

he invested 1/2 at 5%, namely (1/2)a or a/2, and 5% of that is just (5/100) (a/2) or 0.5a/2.

and the rest, hmmm what's the rest? well, 1/2 taken up and then 1/5 taken up, so the rest is the difference of the full amount minus those hmmm let's see


`\bf a-\cfrac{a}{5}-\cfrac{a}{2}\implies \cfrac{10a-2a-5a}{10}\implies \cfrac{3a}{10}`

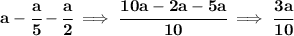
and that was invested at 3.5%, what is 3.5% of that? well is just (3.5/100) * (3a/10), or 0.105a/10.

we know the sum of all those yields was 870 bucks, thus


`\bf \cfrac{0.04a}{5}~~+~~\cfrac{0.05a}{2}~~+~~\cfrac{0.105a}{10}~~=~~870\impliedby \begin{array}{llll} \textit{let's multiply both}\\ \textit{sides by }\stackrel{LCD}{10}~to\\ \textit{toss the denominators} \end{array} \\\\\\ 2(0.04a)+5(0.05a)+0.105a=8700 \\\\\\ 0.08a+0.25a+0.105a=8700\implies 0.435a=8700 \\\\\\ a=\cfrac{8700}{0.435}\implies a=20000`