Question

Suppose that rectangle ABCD is dilated to A'B'C'D' by a scale factor of 0.5 with a center of dilation at (4, 6). What is the distance from the center of dilation to the midpoint of B'C'? A) 0.5 unit B) 1 unit C) 2 units D) 4 units

Answer 1

Answer: The answer is (C) 2 units.

Step-by-step explanation: Given that the rectangle ABCD is dilated about the centre of dilation (4, 6) by a scale factor of 0.5 to form the rectangle A'B'C'D'.

We are to find the distance from the centre of dilation to the midpoint of B'C'.

In the attached figure, we have drawn the dilated rectangle A'B'C'D'. After dilation, the co=-ordinates of the vertices are

A'(3, 5), B'(3, 8), C'(5, 8) and D'(5, 5).

The co-ordinates of the mid-point of B'C' are given by

`((3+5)/(2),(8+8)/(2))=(4,8).`

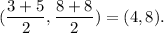
By distance formula, the distance between the points (a,b) and (c,d) is given by

`d=√((c-a)^2+(d-b)^2).`

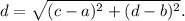
Therefore, the distance between centre of dilation (4,6) and the mid-point of B'C'(4,8) is given by

`d=√((4-4)^2+(8-6)^2)=√(0+4)=2.`

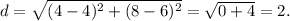
Thus, the required distance is 2 units.

Hence (C) is the correct option.

Answer 2

To solve this problem you must apply the proccedure shown below:

1. You must multiply the coordinates of
`BC` by the scale factor given in the problem above. Therefore, you have that the coordinates of
`B'C'`are:

`B'(1,5)\\ C'(3,5)`

2. The midpoint of
`B'C'` has the folllowing coordinates:

`m((x1+x2)/(2) , (y1+y2)/(2) )\\ m((1+3)/(2), (5+5)/(2))\\ m(2,5)`

3. The center of dilation is a fixed point, with coordinates
`(4,6)`. Therefore, the distance from the center of dilation to the midpoint of
`B'C'` is:

`distance=x2-x1\\distance=4 units-2units\\distance=2 units`

The answer is the option C:
`2 units`