Answer:
The rational exponent form of given expression is
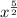 .
.
Explanation:
A number is called a rational number if it can be defined as p/q, where p and q are real numbers and q≠0.
The given expression is
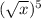
It can be written as
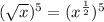
![[\because √(x)=(x)^{(1)/(2)}]](https://img.qammunity.org/2019/formulas/mathematics/high-school/clwzj0h7x0d8x8s7yme87n9b9inrguigr1.png)
Using the power property of exponent we get
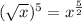
![[\because (x^m)^n=x^(mn)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/619iysagpha2un18uwcj4hj6d25iqgr9a9.png)
Here
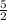 is a rational number.
is a rational number.
Therefore the rational exponent form of given expression is
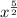 .
.